"Simple —> Complicated —> Simple At first things appear simple. As you learn more they become complicated. As you learn even more, they become simple. Simplicity on the other side of complexity is understanding." - @ShaneAParrish

Beginner = ignorant simplicity Intermediate = functional complexity Advanced = profound simplicity

Excellent adaptation of The Wall by #Sartre youtu.be/uOxehREYiqw

Roger Penrose got the Nobel Prize in Physics!

Buying books would be a good thing if one could also buy the time to read them in. Schopenhauer

For those interested in Bayesian Computation, my friends Gael Martin and Christian Robert and I have just revised our history of Bayesian Computation paper: arxiv.org/abs/2004.06425. The paper should be very helpful for those who are interested in Bayes but unsure where to start!

666 reviews on John Milton's Paradise Lost

To summarise or not to summarise in likelihood-free inference? Find out in my new pre-print with David T. Frazier . @ACEMathStats QUT Centre for Data Science arxiv.org/abs/2103.02407

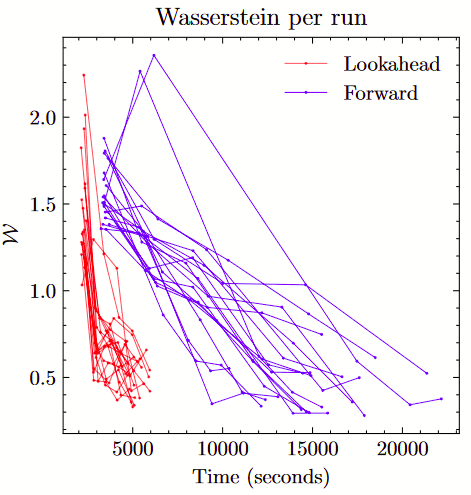
if you are at #ISBA2022, check the poster by Petar Jovanovski: he proposes a very efficient sequential ABC algorithm for SDEs, using carefully constructed "lookahead" trajectories+backward smoothing, and sequentially learned summary statistics.

Everyone knows that all circles are similar. But did you know that all parabolas are similar? The ratio of the red arc and the blue focal segment is √2 + log(1+√2) = 2.29558... for every parabola. This is the universal parabolic constant, the “π of parabolas”.

∫ Today is INTEGRAL DAY ∫ It was on this day 347 years ago [29 Oct 1675] that Leibniz has written down the first ever integral sign ∫ Celebrate this day by sharing your favourite integral or integral related fact / content.

Our new youTube channel: youtube.com/playlist?list=… Comments welcome!