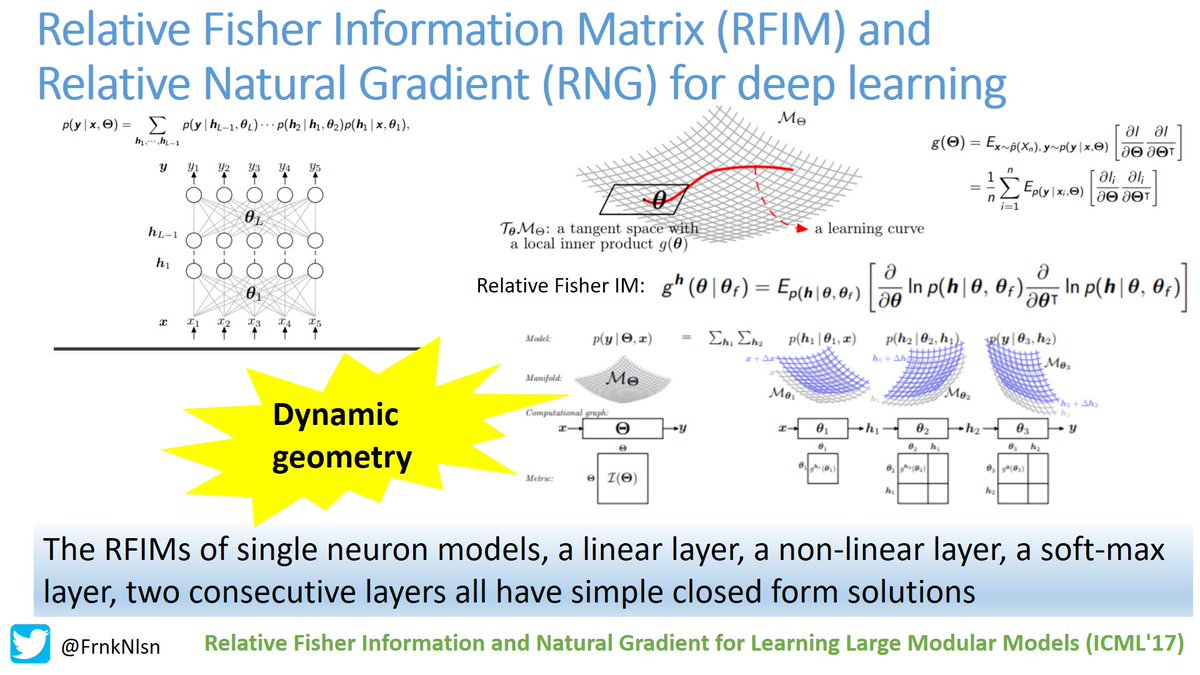
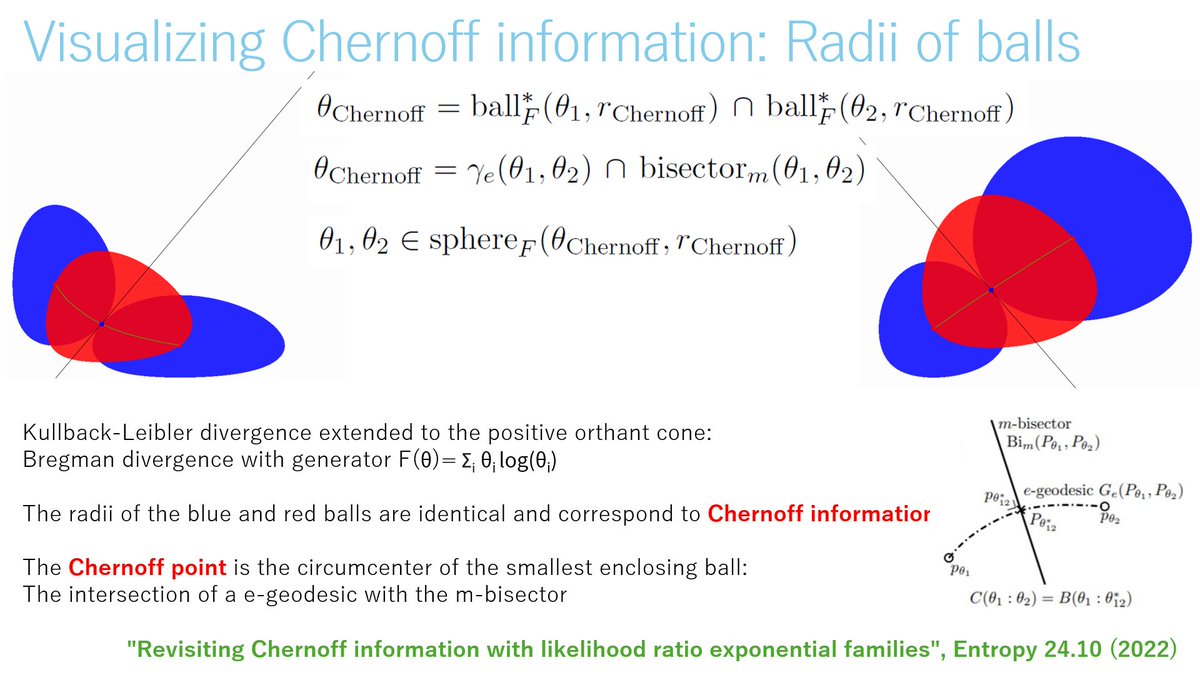
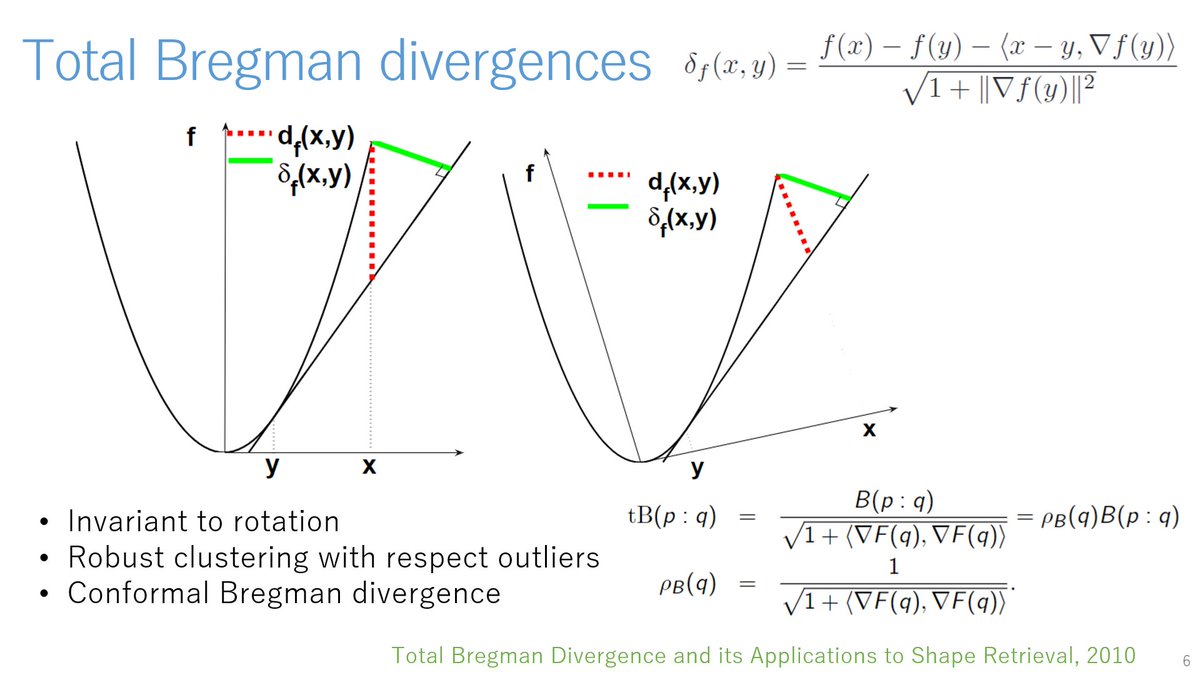
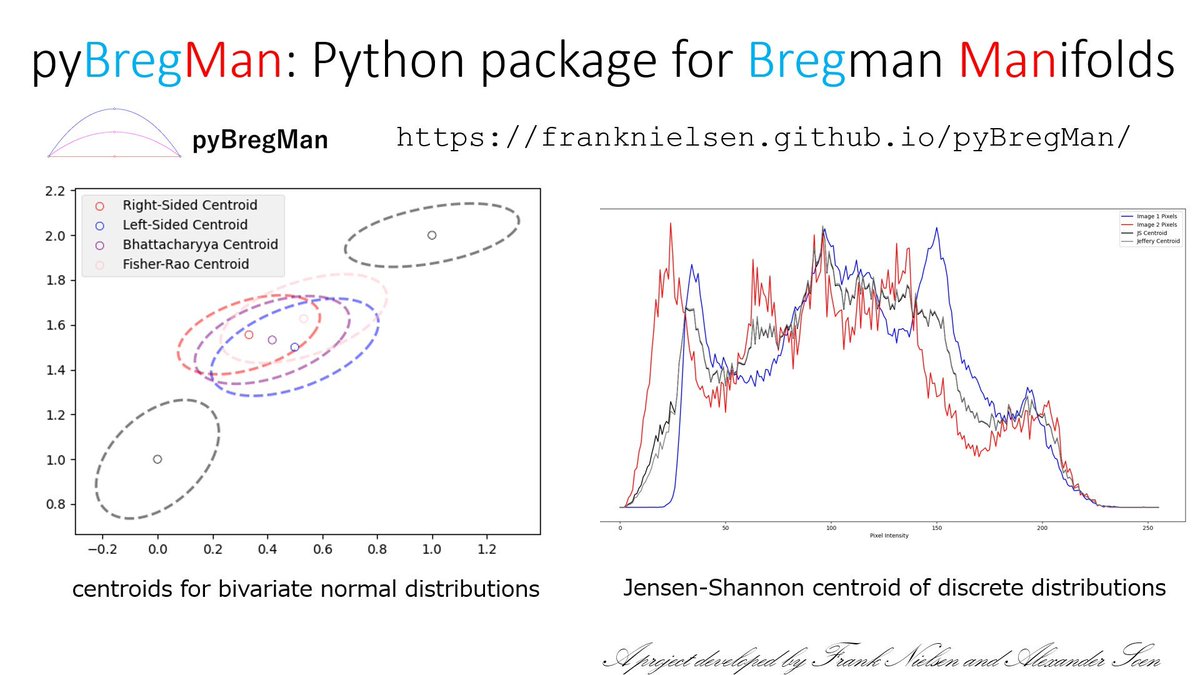
Frank Nielsen
@frnknlsn
Geometric Science of Information (GSI) and Information Geometry for machine learning and AI, visual computing, HPC, and more! pyBregMan library. @SonyCSL
ID: 117258094
https://franknielsen.github.io/index.html 25-02-2010 01:38:54
6,6K Tweet
32,32K Followers
1,1K Following















![Frank Nielsen (@frnknlsn) on Twitter photo Paper by Prof Amari (1991) with quotes:
"... [new unifying method to information sciences] to provide a new unifying method to information sciences.''
``It opens a new field called information geometry.''
``This papers opens a new fertile field of neural network research.'' Paper by Prof Amari (1991) with quotes:
"... [new unifying method to information sciences] to provide a new unifying method to information sciences.''
``It opens a new field called information geometry.''
``This papers opens a new fertile field of neural network research.''](https://pbs.twimg.com/media/Gu7olPyXYAEsdI6.png)