Check out our new preprint on universal error corrected operations of bosonic qubits with noisy ancillae arxiv.org/abs/2310.20578. Made it just in time before my talk at #qec23! Please come to my talk today if you are interested!

qLDPC codes reduce space overhead for fault tolerance, but logical computations with them often require serialized operations, increasing time costs. Looking for more efficient logical operations? Check out our new work arxiv.org/abs/2407.18490! (1/6)

This work demonstrates that Gottesman-Kitaev-Preskill codes are the first structured bosonic codes proven to achieve optimal quantum communication rates under realistic noise models. Jerry Zheng go.aps.org/4f6FOrg

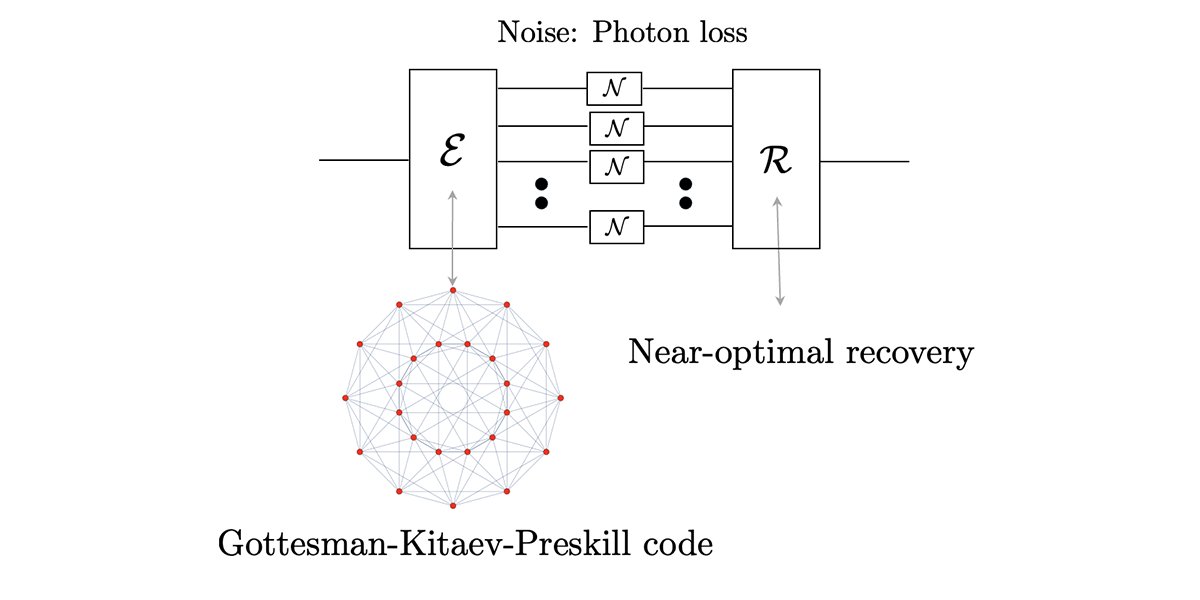
Researchers at @uchicagopme, @mit, Amazon Web Services show that the performance of GKP codes — which are useful for #quantum error correction — is closely tied to the geometry of their structure and the amount of energy put into them. journals.aps.org/prxquantum/abs…

Our work "Error-structure-tailored early fault-tolerant quantum computing" is finally out! In this work, we have shown how to perform the continuous logical-rotation gates Rz(\phi) as simple as CNOT, but still with good accuracy! scirate.com/arxiv/2511.199…