Unfortunately, yesterday the registration website of the 2022 World Meeting #ISBA2022 experienced some technical issues. The early-bird registration deadline has been postponed to April 15. Conference website: isbawebmaster.github.io/ISBA2022/

ISBA announces a call for pre-proposals for the ISBA World Meetings in 2026 and 2028. We encourage any interested members to contribute to the main scientific gathering of our society by submitting a pre-proposal to the ISBA Program Council. Deadline: October 31, 2022.

Multiple interpretations of ambiguous percept must be associated with multiple values of an explanatory latent variable. By *latent*, I mean that they are not outputs but internal inputs. What are the mechanisms in the brain for exploring the set of plausible values?

I have an open postdoc position in Mathematical Statistics at Bocconi University (Milano). Deadline: 4th of December, 2022. Application link: jobmarket.unibocconi.eu/?type=a&urlBac…

The skewed Bernstein-von Mises theorem is online arxiv.org/abs/2301.03038. With Francesco Pozza and Botond Szabo we derive a new limiting law given by tractable generalized skew-normals that remarkably improves the convergence rate (and practical accuracy) of the classical BvM result!

🚨1 PhD position in high-dimensional #causal inference with @stephanievdpas Amsterdam UMC as part of her European Research Council (ERC) Starting Grant🚨 We will try to combine reliable causal discovery and effect estimation in high-dimensional settings. Deadline: April 2 werkenbij.amsterdamumc.org/en/vacatures/r…

***PLEASE SHARE*** I am looking for a PhD student to work on machine learning theory at UPF Barcelona Deadline: May 26 More info: cs.bme.hu/~gergo/jobs.ht…

Hey twitter #stats, is there anybody in there? 🎶 We have just been funded for #RISE: Rethinking and Innovating Statistics for Extremes 📈

academicjobsonline.org/ajo/jobs/25471 New Postdoc position in my group at Duke University. Please let people know!

Understanding and combating criminal networks - Daniele Durante has secured European Research Council (ERC) funding to develop cutting-edge statistical models & methods for studying their mechanisms & dynamics #KnowledgeThatMatters #ERCStG knowledge.unibocconi.eu/notizia.php?id…

I have an open postdoc position in mathematical statistics at Bocconi (application deadline: 31st of January): If you are interested send me an email or apply directly at: jobmarket.unibocconi.eu/application.ph…

‼️ Less than a week left to apply for a postdoc within the ERC project NEMESIS (tinyurl.com/4d2ry2vj). 🔍Goal: Develop advanced models and methods for the analysis of complex (multiplex, multilayer, dynamic, ...) criminal networks 🕵️. More info (jobmarket.unibocconi.eu/?id=574) 👇

I have an open postdoc position at Bocconi on theory for scalable statistical methods. Application deadline is the 8th of July. jobmarket.unibocconi.eu/?type=a (ID 604)

🤩 Congratulations to my former PhD student Francesco Pozza who received the Laplace award 🏆 at #JSM2024, for the article "skewed Bernstein-von Mises theorem and skew-modal approximations" (arxiv.org/abs/2301.03038) (recently accepted for publication in the Annals of Statistics ‼️)

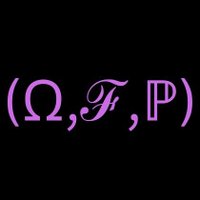
Paper: Skewed Bernstein-Von Mises Theorem and Skew-Modal Approximations Accepted in Annals of Statistics Authors: Daniele Durante Francesco Pozza Botond Szabo

😎 For any, already-derived, symmetric approximation of a generic posterior distribution, we provide, at no additional optimization costs, a similarly-tractable, yet provably more accurate, skew-symmetric approximation! (arxiv.org/abs/2409.14167) (with Francesco Pozza and Botond Szabo)

At Bocconi University (Milano, Italy) we have an open tenure-track position at the Assistant Professor level in Statistics. If interested, you can apply at jobmarket.unibocconi.eu Application deadline: 15th of December, 23:59 (CET).

I have two postdoc positions in mathematical statistics at Bocconi (application deadline: 15th of January). Application link and detailed description here: jobmarket.unibocconi.eu/?id=703