I'm excited to announce basic support for ResNets & RNNs in BackPACK 1.4 for PyTorch! 🎉 Find out more in the tutorials: 📈 docs.backpack.pt/en/1.4.0/use_c… 📈 docs.backpack.pt/en/1.4.0/use_c… Thanks to Tim Schäfer for his work on the library in the past months 🙏.

In our #NeurIPS2021 paper (arxiv.org/abs/2106.14806), we introduce laplace-torch for effortless Bayesian deep learning. Despite their simplicity, we find that Laplace approximations are surprisingly competitive with more popular approaches. youtu.be/nMONiYLWWOU

Which plane would you board? [#NeurIPS2021] Cockpit: Practical trouble-shooting of DNN training. Empowered by recent advances in autodiff. In collaboration with Frank Schneider & @PhilippHennig5.

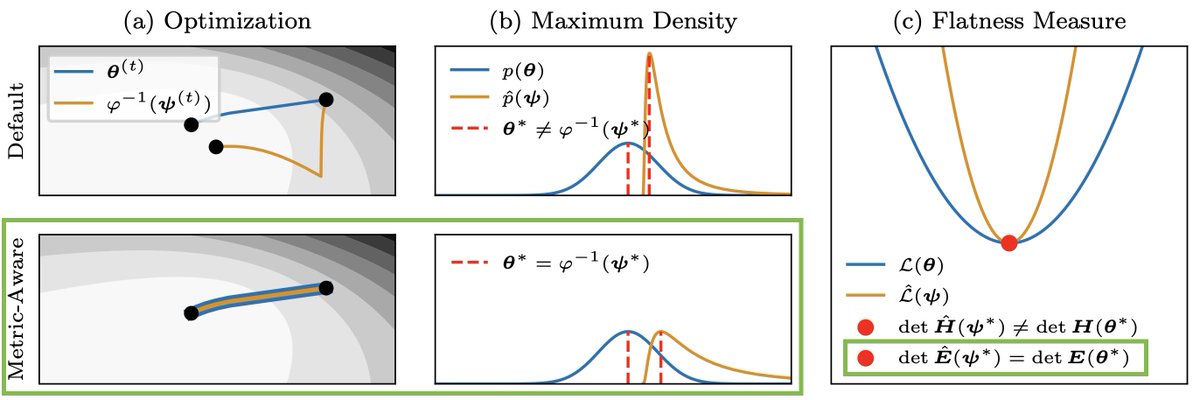
The consensus in deep learning is that many quantities are not invariant under reparametrization. Our #NeurIPS2023 paper shows that they actually are if the implicitly assumed Riemannian metric is taken into account 🧵 arxiv.org/abs/2302.07384 w/ Felix Dangel and @PhilippHennig5

For the first time, we (with Felix Dangel, Runa Eschenhagen, Kirill Neklyudov Agustinus Kristiadi, Richard E. Turner, Alireza Makhzani) propose a sparse 2nd-order method for large NN training with BFloat16 and show its advantages over AdamW. also @NeurIPS workshop on Opt for ML arxiv.org/abs/2312.05705 /1

#ICML2024 Can We Remove the Square-Root in Adaptive Methods? arxiv.org/abs/2402.03496 Root-free (RF) methods are better on CNNs and competitive on Transformers compared to root-based methods (AdamW) Removing the root makes matrix methods faster: Root-free Shampoo in BFloat16 /1

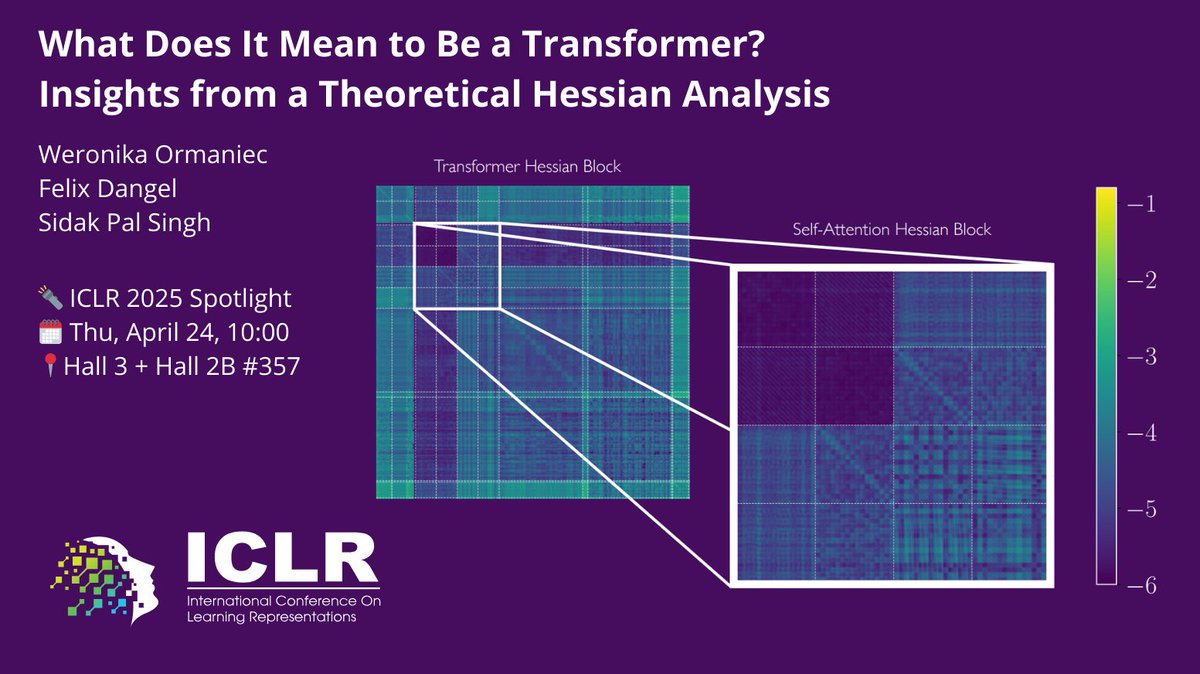
Ever wondered how the loss landscape of Transformers differs from that of other architectures? Or which Transformer components make its loss landscape unique? With Sidak Pal Singh & Felix Dangel, we explore this via the Hessian in our #ICLR2025 spotlight paper! Key insights👇 1/8

KFAC is everywhere—from optimization to influence functions. While the intuition is simple, implementation is tricky. We (Bálint Mucsányi, Tobias Weber ,Runa Eschenhagen) wrote a ground-up intro with code to help you get it right. 📖 arxiv.org/abs/2507.05127 💻 github.com/f-dangel/kfac-…